Papers
My papers are also listed on my Google Scholar and Semantic Scholar.

Highly Accurate Real-space Electron Densities with Neural Networks
Lixue Cheng, P. Bernát Szabó, Zeno Schätzle, Derk Kooi, Jonas Köhler, Klaas J. H. Giesbertz, Frank Noé, Jan Hermann, Paola Gori-Giorgi, Adam Foster. Journal of Chemical Physics.
Variational ab-initio methods in quantum chemistry stand out among other methods in providing direct access to the wave function. This allows in principle straightforward extraction of any other observable of interest, besides the energy, but in practice this extraction is often technically difficult and computationally impractical. Here, we consider the electron density as a central observable in quantum chemistry and introduce a novel method to obtain accurate densities from real-space many-electron wave functions by representing the density with a neural network that captures known asymptotic properties and is trained from the wave function by score matching and noise-contrastive estimation. We use variational quantum Monte Carlo with deep-learning ansätze (deep QMC) to obtain highly accurate wave functions free of basis set errors, and from them, using our novel method, correspondingly accurate electron densities, which we demonstrate by calculating dipole moments, nuclear forces, contact densities, and other density-based properties.
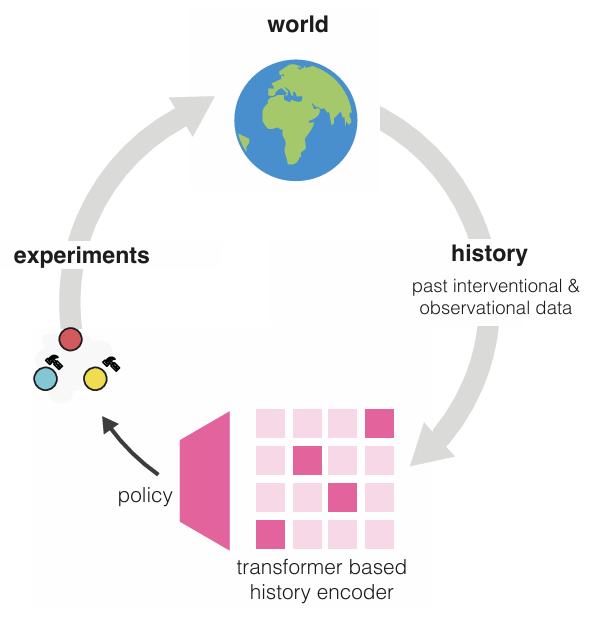
Amortized Active Causal Induction with Deep Reinforcement Learning
Yashas Annadani, Panagiotis Tigas, Stefan Bauer, Adam Foster. NeurIPS 2024.
We present Causal Amortized Active Structure Learning (CAASL), an active intervention design policy that can select interventions that are adaptive, real-time and that does not require access to the likelihood. This policy, an amortized network based on the transformer, is trained with reinforcement learning on a simulator of the design environment, and a reward function that measures how close the true causal graph is to a causal graph posterior inferred from the gathered data. On synthetic data and a single-cell gene expression simulator, we demonstrate empirically that the data acquired through our policy results in a better estimate of the underlying causal graph than alternative strategies. Our design policy successfully achieves amortized intervention design on the distribution of the training environment while also generalizing well to distribution shifts in test-time design environments. Further, our policy also demonstrates excellent zero-shot generalization to design environments with dimensionality higher than that during training, and to intervention types that it has not been trained on.
-
Making Better Use of Unlabelled Data in Bayesian Active Learning
Freddie Bickford Smith, Adam Foster, Tom Rainforth. AISTATS 2024.
Fully supervised models are predominant in Bayesian active learning. We argue that their neglect of the information present in unlabelled data harms not just predictive performance but also decisions about what data to acquire. Our proposed solution is a simple framework for semi-supervised Bayesian active learning. We find it produces better-performing models than either conventional Bayesian active learning or semi-supervised learning with randomly acquired data. It is also easier to scale up than the conventional approach. As well as supporting a shift towards semi-supervised models, our findings highlight the importance of studying models and acquisition methods in conjunction.
Prediction-Oriented Bayesian Active Learning
Freddie Bickford Smith, Andreas Kirsch, Sebastian Farquhar, Yarin Gal, Adam Foster, Tom Rainforth. AISTATS 2023.
Information-theoretic approaches to active learning have traditionally focused on maximising the information gathered about the model parameters, most commonly by optimising the BALD score. We highlight that this can be suboptimal from the perspective of predictive performance. For example, BALD lacks a notion of an input distribution and so is prone to prioritise data of limited relevance. To address this we propose the expected predictive information gain (EPIG), an acquisition function that measures information gain in the space of predictions rather than parameters. We find that using EPIG leads to stronger predictive performance compared with BALD across a range of datasets and models, and thus provides an appealing drop-in replacement.
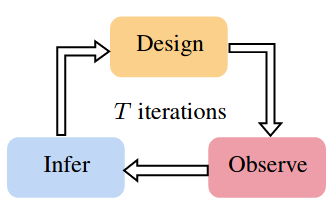
Modern Bayesian Experimental Design
Tom Rainforth, Adam Foster, Desi R Ivanova, Freddie Bickford Smith. Statistical Science.
Bayesian experimental design (BED) provides a powerful and general framework for optimizing the design of experiments. However, its deployment often poses substantial computational challenges that can undermine its practical use. In this review, we outline how recent advances have transformed our ability to overcome these challenges and thus utilize BED effectively, before discussing some key areas for future development in the field.
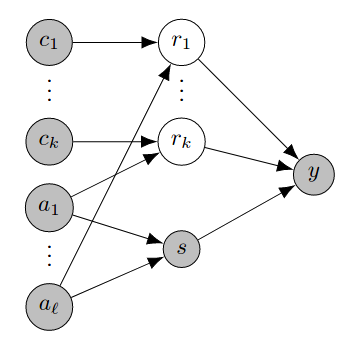
CO-BED: Information-Theoretic Contextual Optimization via Bayesian Experimental Design
Desi R Ivanova, Joel Jennings, Tom Rainforth, Cheng Zhang, Adam Foster. ICML 2023.
We formalize the problem of contextual optimization through the lens of Bayesian experimental design and propose CO-BED - a general, model-agnostic framework for designing contextual experiments using information-theoretic principles. After formulating a suitable information-based objective, we employ black-box variational methods to simultaneously estimate it and optimize the designs in a single stochastic gradient scheme. We further introduce a relaxation scheme to allow discrete actions to be accommodated. As a result, CO-BED provides a general and automated solution to a wide range of contextual optimization problems. We illustrate its effectiveness in a number of experiments, where CO-BED demonstrates competitive performance even when compared to bespoke, model-specific alternatives.
Differentiable Multi-Target Causal Bayesian Experimental Design
Yashas Annadani, Panagiotis Tigas, Desi R. Ivanova, Andrew Jesson, Yarin Gal, Adam Foster, Stefan Bauer. ICML 2023.
We introduce a gradient-based approach for the problem of Bayesian optimal experimental design to learn causal models in a batch setting – a critical component for causal discovery from finite data where interventions can be costly or risky. Existing methods rely on greedy approximations to construct a batch of experiments while using black-box methods to optimize over a single target-state pair to intervene with. In this work, we completely dispose of the black-box optimization techniques and greedy heuristics and instead propose a conceptually simple end-to-end gradient-based optimization procedure to acquire a set of optimal intervention target-state pairs. Such a procedure enables parameterization of the design space to efficiently optimize over a batch of multi-target-state interventions, a setting which has hitherto not been explored due to its complexity. We demonstrate that our proposed method outperforms baselines and existing acquisition strategies in both single-target and multi-target settings across a number of synthetic datasets.
Efficient Real-world Testing of Causal Decision Making via Bayesian Experimental Design for Contextual Optimisation
Desi R. Ivanova, Joel Jennings, Cheng Zhang, Adam Foster. ICML 2022 Workshop on Adaptive Experimental Design and Active Learning in the Real World.
The real-world testing of decisions made using causal machine learning models is an essential prerequisite for their successful application. We focus on evaluating and improving contextual treatment assignment decisions: these are personalised treatments applied to e.g. customers, each with their own contextual information, with the aim of maximising a reward. In this paper we introduce a model-agnostic framework for gathering data to evaluate and improve contextual decision making through Bayesian Experimental Design. Specifically, our method is used for the data-efficient evaluation of the regret of past treatment assignments. Unlike approaches such as A/B testing, our method avoids assigning treatments that are known to be highly sub-optimal, whilst engaging in some exploration to gather pertinent information. We achieve this by introducing an information-based design objective, which we optimise end-to-end. Our method applies to discrete and continuous treatments. Comparing our information-theoretic approach to baselines in several simulation studies demonstrates the superior performance of our proposed approach.
Learning Instance-Specific Augmentations by Capturing Local Invariances
Ning Miao, Tom Rainforth, Emile Mathieu, Yann Dubois, Yee Whye Teh, Adam Foster, Hyunjik Kim. ICML 2023.
We introduce InstaAug, a method for automatically learning input-specific augmentations from data. Previous methods for learning augmentations have typically assumed independence between the original input and the transformation applied to that input. This can be highly restrictive, as the invariances we hope our augmentation will capture are themselves often highly input dependent. InstaAug instead introduces a learnable invariance module that maps from inputs to tailored transformation parameters, allowing local invariances to be captured. This can be simultaneously trained alongside the downstream model in a fully end-to-end manner, or separately learned for a pre-trained model. We empirically demonstrate that InstaAug learns meaningful input-dependent augmentations for a wide range of transformation classes, which in turn provides better performance on both supervised and self-supervised tasks.

DPhil Thesis: Variational, Monte Carlo and Policy-Based Approaches to Bayesian Experimental Design
Adam Foster. University of Oxford.
Experimentation is key to learning about our world, but careful design of experiments is critical to ensure resources are used efficiently to conduct discerning investigations. Bayesian experimental design (BED) is an elegant framework that provides a mathematical definition of the expected information gain (EIG) of running a certain experiment. Finding the design with the maximal EIG will, in expectation, give experimental outcomes that are most informative about the underlying phenomenon. BED promises to launch a revolution in science and machine learning, but it is only beginning to realise its potential due to numerous unsolved computational problems. One fundamental computational issue is the estimation of EIG, where a naïve approach necessitates nested calculation of Bayesian posteriors. Further computational challenges concern the optimisation of the EIG across design space, and the design of adaptive experiments that use data that has been already observed to find the optimal design of the next experiment. In this thesis, we ask whether the machinery of modern machine learning can be brought to bear on these computational challenges, demonstrating that significant advances are possible when modern ML is combined with a deep understanding of BED. We begin by examining the EIG estimation problem, being the first to apply variational inference and inference amortisation to the problem. We then turn to optimisation of the EIG over a continuous design space, showing that stochastic gradient methods, which have not been widely adopted in BED, combine with simultaneous optimisation of variational parameters to great effect. Continuing on this theme, we show that it is possible to obtain unbiased gradients of EIG using Multi-level Monte Carlo. For the adaptive design problem, a key limitation of most methods is that they require substantial computation at each iteration of the experiment. We ask whether this process itself cannot be amortised, ultimately deriving an algorithm that trains a design policy network offline to be deployed with lightning-fast design decisions during a live experiment. Finally, we show how this policy-driven approach extends to implicit models. Together, these contributions move the field of Bayesian experimental design forward significantly in terms of what is computationally possible. Our hope is that practitioners will be able to apply these ideas to advance human understanding in many scientific disciplines.
Deep End-to-end Causal Inference
Tomas Geffner, Javier Antoran, Adam Foster, Wenbo Gong, Chao Ma, Emre Kiciman, Amit Sharma, Angus Lamb, Martin Kukla, Nick Pawlowski, Miltiadis Allamanis, Cheng Zhang. Transactions on Machine Learning Research.
Causal inference is essential for data-driven decision making across domains such as business engagement, medical treatment or policy making. However, research on causal discovery and inference has evolved separately, and the combination of the two domains is not trivial. In this work, we develop Deep End-to-end Causal Inference (DECI), a single flow-based method that takes in observational data and can perform both causal discovery and inference, including conditional average treatment effect (CATE) estimation. We provide a theoretical guarantee that DECI can recover the ground truth causal graph under mild assumptions. In addition, our method can handle heterogeneous, real-world, mixed-type data with missing values, allowing for both continuous and discrete treatment decisions. Moreover, the design principle of our method can generalize beyond DECI, providing a general End-to-end Causal Inference (ECI) recipe, which enables different ECI frameworks to be built using existing methods. Our results show the superior performance of DECI when compared to relevant baselines for both causal discovery and (C)ATE estimation in over a thousand experiments on both synthetic datasets and other causal machine learning benchmark datasets.

Implicit Deep Adaptive Design: Policy-Based Experimental Design without Likelihoods
Desi R. Ivanova, Adam Foster, Steven Kleinegesse, Michael U. Gutmann, Tom Rainforth. NeurIPS 2021.
We introduce implicit Deep Adaptive Design (iDAD), a new method for performing adaptive experiments in real-time with implicit models. iDAD amortizes the cost of Bayesian optimal experimental design (BOED) by learning a design policy network upfront, which can then be deployed quickly at the time of the experiment. The iDAD network can be trained on any model which simulates differentiable samples, unlike previous design policy work that requires a closed form likelihood and conditionally independent experiments. At deployment, iDAD allows design decisions to be made in milliseconds, in contrast to traditional BOED approaches that require heavy computation during the experiment itself. We illustrate the applicability of iDAD on a number of experiments, and show that it provides a fast and effective mechanism for performing adaptive design with implicit models.

On Contrastive Representations of Stochastic Processes
Emile Mathieu, Adam Foster, Yee Whye Teh. NeurIPS 2021.
Learning representations of stochastic processes is an emerging problem in machine learning with applications from meta-learning to physical object models to time series. Typical methods rely on exact reconstruction of observations, but this approach breaks down as observations become high-dimensional or noise distributions become complex. To address this, we propose a unifying framework for learning contrastive representations of stochastic processes (CRESP) that does away with exact reconstruction. We dissect potential use cases for stochastic process representations, and propose methods that accommodate each. Empirically, we show that our methods are effective for learning representations of periodic functions, 3D objects and dynamical processes. Our methods tolerate noisy high-dimensional observations better than traditional approaches, and the learned representations transfer to a range of downstream tasks.
Contrastive Mixture of Posteriors for Counterfactual Inference, Data Integration and Fairness
Adam Foster, Árpi Vezér, Craig A Glastonbury, Páidí Creed, Sam Abujudeh, Aaron Sim. ICML 2022 (long presentation).
Learning meaningful representations of data that can address challenges such as batch effect correction, data integration and counterfactual inference is a central problem in many domains including computational biology. Adopting a Conditional VAE framework, we identify the mathematical principle that unites these challenges: learning a representation that is marginally independent of a condition variable. We therefore propose the Contrastive Mixture of Posteriors (CoMP) method that uses a novel misalignment penalty to enforce this independence. This penalty is defined in terms of mixtures of the variational posteriors themselves, unlike prior work which uses external discrepancy measures such as MMD to ensure independence in latent space. We show that CoMP has attractive theoretical properties compared to previous approaches, especially when there is complex global structure in latent space. We further demonstrate state of the art performance on a number of real-world problems, including the challenging tasks of aligning human tumour samples with cancer cell-lines and performing counterfactual inference on single-cell RNA sequencing data. Incidentally, we find parallels with the fair representation learning literature, and demonstrate CoMP has competitive performance in learning fair yet expressive latent representations.
Deep Adaptive Design: Amortizing Sequential Bayesian Experimental Design
Adam Foster, Desi R. Ivanova, Ilyas Malik, Tom Rainforth. ICML 2021 (long presentation).
We introduce Deep Adaptive Design (DAD), a general method for amortizing the cost of performing sequential adaptive experiments using the framework of Bayesian optimal experimental design (BOED). Traditional sequential BOED approaches require substantial computational time at each stage of the experiment. This makes them unsuitable for most real-world applications, where decisions must typically be made quickly. DAD addresses this restriction by learning an amortized design network upfront and then using this to rapidly run (multiple) adaptive experiments at deployment time. This network takes as input the data from previous steps, and outputs the next design using a single forward pass; these design decisions can be made in milliseconds during the live experiment. To train the network, we introduce contrastive information bounds that are suitable objectives for the sequential setting, and propose a customized network architecture that exploits key symmetries. We demonstrate that DAD successfully amortizes the process of experimental design, outperforming alternative strategies on a number of problems.
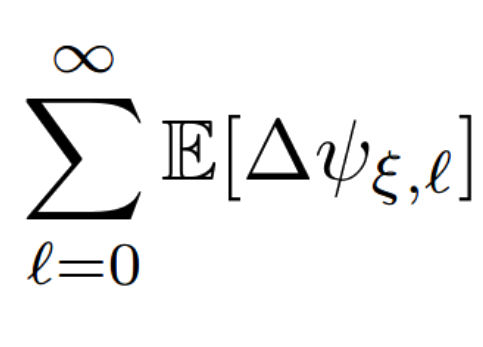
Unbiased MLMC stochastic gradient-based optimization of Bayesian experimental designs
Takashi Goda, Tomohiko Hironaka, Wataru Kitade, Adam Foster. SIAM Journal on Scientific Computing.
In this paper we propose an efficient stochastic optimization algorithm to search for Bayesian experimental designs such that the expected information gain is maximized. The gradient of the expected information gain with respect to experimental design parameters is given by a nested expectation, for which the standard Monte Carlo method using a fixed number of inner samples yields a biased estimator. In this paper, applying the idea of randomized multilevel Monte Carlo (MLMC) methods, we introduce an unbiased Monte Carlo estimator for the gradient of the expected information gain with finite expected squared ℓ2-norm and finite expected computational cost per sample. Our unbiased estimator can be combined well with stochastic gradient descent algorithms, which results in our proposal of an optimization algorithm to search for an optimal Bayesian experimental design. Numerical experiments confirm that our proposed algorithm works well not only for a simple test problem but also for a more realistic pharmacokinetic problem.

Improving Transformation Invariance in Contrastive Representation Learning
Adam Foster, Rattana Pukdee, Tom Rainforth. ICLR 2021.
We propose methods to strengthen the invariance properties of representations obtained by contrastive learning. While existing approaches implicitly induce a degree of invariance as representations are learned, we look to more directly enforce invariance in the encoding process. To this end, we first introduce a training objective for contrastive learning that uses a novel regularizer to control how the representation changes under transformation. We show that representations trained with this objective perform better on downstream tasks and are more robust to the introduction of nuisance transformations at test time. Second, we propose a change to how test time representations are generated by introducing a feature averaging approach that combines encodings from multiple transformations of the original input, finding that this leads to across the board performance gains. Finally, we introduce the novel Spirograph dataset to explore our ideas in the context of a differentiable generative process with multiple downstream tasks, showing that our techniques for learning invariance are highly beneficial.
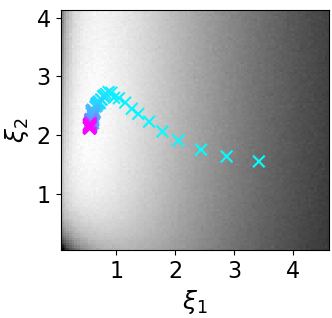
A Unified Stochastic Gradient Approach to Designing Bayesian-Optimal Experiments
Adam Foster, Martin Jankowiak, Matthew O'Meara, Yee Whye Teh, Tom Rainforth. AISTATS 2020.
We introduce a fully stochastic gradient based approach to Bayesian optimal experimental design (BOED). Our approach utilizes variational lower bounds on the expected information gain (EIG) of an experiment that can be simultaneously optimized with respect to both the variational and design parameters. This allows the design process to be carried out through a single unified stochastic gradient ascent procedure, in contrast to existing approaches that typically construct a pointwise EIG estimator, before passing this estimator to a separate optimizer. We provide a number of different variational objectives including the novel adaptive contrastive estimation (ACE) bound. Finally, we show that our gradient-based approaches are able to provide effective design optimization in substantially higher dimensional settings than existing approaches.

Variational Bayesian Optimal Experimental Design
Adam Foster, Martin Jankowiak, Eli Bingham, Paul Horsfall, Yee Whye Teh, Tom Rainforth, Noah D Goodman. NeurIPS 2019 (spotlight).
Bayesian optimal experimental design (BOED) is a principled framework for making efficient use of limited experimental resources. Unfortunately, its applicability is hampered by the difficulty of obtaining accurate estimates of the expected information gain (EIG) of an experiment. To address this, we introduce several classes of fast EIG estimators by building on ideas from amortized variational inference. We show theoretically and empirically that these estimators can provide significant gains in speed and accuracy over previous approaches. We further demonstrate the practicality of our approach on a number of end-to-end experiments.
-
Variational Optimal Experiment Design: Efficient Automation of Adaptive Experiments
Adam Foster, Martin Jankowiak, Eli Bingham, Yee Whye Teh, Tom Rainforth, Noah D Goodman. NeurIPS 2018 Workshop on Bayesian Deep Learning.
Bayesian optimal experimental design (OED) is a principled framework for making efficient use of limited experimental resources. Unfortunately, the applicability of OED is hampered by the difficulty of obtaining accurate estimates of the expected information gain (EIG) for different experimental designs. We introduce a class of fast EIG estimators that leverage amortised variational inference and show that they provide substantial empirical gains over previous approaches. We integrate our approach into a deep probabilistic programming framework, thus making OED accessible to practitioners at large.
-
Sampling and Inference for Beta Neutral-to-the-Left Models of Sparse Networks
Benjamin Bloem-Reddy, Adam Foster, Emile Mathieu, Yee Whye Teh. UAI 2018.
Empirical evidence suggests that heavy-tailed degree distributions occurring in many real networks are well-approximated by power laws with exponents η that may take values either less than and greater than two. Models based on various forms of exchangeability are able to capture power laws with η<2, and admit tractable inference algorithms; we draw on previous results to show that η>2 cannot be generated by the forms of exchangeability used in existing random graph models. Preferential attachment models generate power law exponents greater than two, but have been of limited use as statistical models due to the inherent difficulty of performing inference in non-exchangeable models. Motivated by this gap, we design and implement inference algorithms for a recently proposed class of models that generates η of all possible values. We show that although they are not exchangeable, these models have probabilistic structure amenable to inference. Our methods make a large class of previously intractable models useful for statistical inference.
-
Sampling and inference for discrete random probability measures in probabilistic programs
Benjamin Bloem-Reddy, Emile Mathieu, Adam Foster, Tom Rainforth, Yee Whye Teh, Hong Ge, María Lomelí, Zoubin Ghahramani. NeurIPS 2017 Workshop on Advances in Approximate Bayesian Inference.
We consider the problem of sampling a sequence from a discrete random probability measure (RPM) with countable support, under (probabilistic) constraints of finite memory and computation. A canonical example is sampling from the Dirichlet Process, which can be accomplished using its stick-breaking representation and lazy initialization of its atoms. We show that efficiently lazy initialization is possible if and only if a size-biased representation of the discrete RPM is used. For models constructed from such discrete RPMs, we consider the implications for generic particle-based inference methods in probabilistic programming systems. To demonstrate, we implement SMC for Normalized Inverse Gaussian Process mixture models in Turing.