Posts
A machine learning introduction to Orbformer
Adam Foster. Blog post.
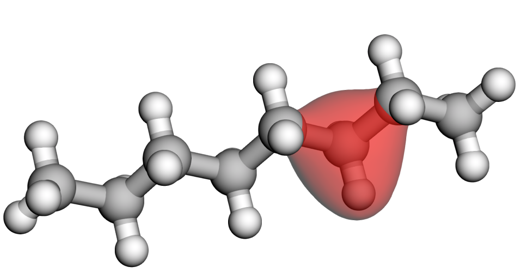
We have just released Orbformer, a foundation model of molecular wavefunctions! This is a project I have been working on over the last two-and-a-bit years as part of an amazing team. This blog post tells the story of Orbformer from a machine learning perspective, filling in some quantum chemistry details along the way.
Stochastic-gradient Bayesian Optimal Experimental Design with Gaussian Processes
Adam Foster. Blog post.
A couple of people have asked me how Gaussian Process (GP) models can be incorporated into the framework of Stochastic Gradient Bayesian Optimal Experimental Design (SGBOED) and Deep Adaptive Design (DAD). Where a lot of older work on experimental design and particularly Bayesian optimisation only works for GP models, it seems prima facie that SGBOED does not work for GPs or any nonparametric Bayesian models. In this post, I’ll show conceptually that SGBOED works with GPs. There is also a Pyro code example. In a subsequent post I will look into more exotic models that incorporate GPs, as well as adaptivity and other objective functions for learning designs.
Optimising adaptive experimental designs with RL
Adam Foster. Blog post.
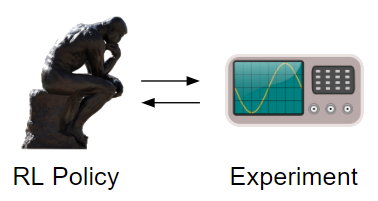
This post follows up on a previous one which discussed the connection between Reinforcement Learning (RL) and Deep Adaptive Design (DAD). Here, I am taking a deeper dive into two 2022 papers that build off of DAD and use RL to train policies for adaptive experimental design: Blau et al. and Lim et al.. This is both a natural and interesting direction because training with RL removes some of the major limitations of DAD, such as struggling to handle non-differentiable models and discrete design spaces, and allows us to tap into advances in RL to optimise design policies.

Deep Adaptive Design and Bayesian reinforcement learning
Adam Foster. Blog post.
This post discusses the connection between one of my own papers, Deep Adaptive Design (DAD), and the field of Bayesian reinforcement learning. That such a connection exists is hinted at by a high-level appraisal of the DAD method: it solves a sequential decision making problem to optimise a certain objective function, decision optimality is dependent on a state which is the experimental data already gathered, and the automated decision maker is a design policy network. We begin by showing how the sequential Bayesian experimental design problem solved by DAD can be viewed as a Bayes Adaptive Markov Decision Process (BAMDP), making this connection formally precise. There are also key differences between the problem DAD is solving and a conventional Bayesian RL problem, in particular, the reward in DAD is intractable.
Given this connection, the question arises “what use can we make of it?” First, there are rather natural extensions of DAD to more general objective functions. Second, it should be possible to apply standard RL techniques, such as Q-learning and policy optimization to the sequential Bayesian experimental design problem, which may be particularly useful for long- or infinite-horizon problems.
BALD and BED: Connecting Bayesian active learning by disagreement and Bayesian experimental design
Adam Foster. Blog post.
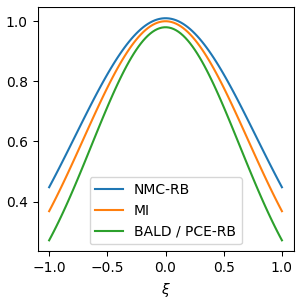
There is a deep connection between Bayesian experimental design and Bayesian active learning. A significant touchpoint is the use of the mutual information score as an acquisition function \(I(\xi) = \mathbb{E}_{p(\theta)p(y\mid \theta,\xi)}\left[H[p(\theta)] - H[p(\theta\mid y,\xi)]\right]\) which is also called the Expected Information Gain. In this equation, \(\theta\) are the Bayesian model parameters, \(y\) is the as yet unobserved outcome, and \(\xi\) is the design to be chosen. In the DBALD paper, Gal et al. introduced a means to estimate the mutual information acquisition function \(I(\xi)\) for active learning when using an MC Dropout-driven Bayesian neural network. In recent work on variational and stochastic gradient Bayesian experimental design, my collaborators and I studied estimators of the mutual information—including one in particular called Prior Constrative Estimation (PCE). Whilst the DBALD estimator and PCE look different on the surface, it turns out they have the same expectation and are almost identical: one is simply a Rao-Blackwellised version of the other. Which proves that the expectation of DBALD is always a lower bound on the true mutual information, which goes some way to explaining the stability of BALD as an acquisition function. Using this finding, we show that BALD actually has an upper bound “cousin” estimator.
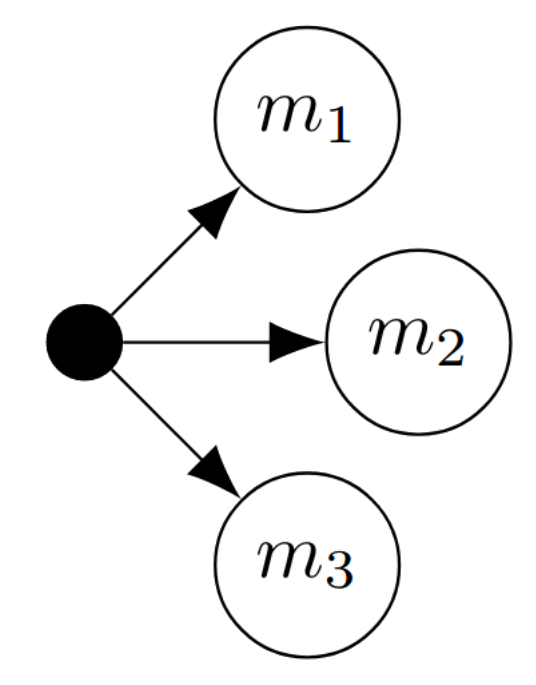
Bayesian experimental design for model selection: variational and classification approaches
Adam Foster. Blog post.
This post focuses on a particular use case for Bayesian experimental design: designing experiments for model selection. We set out to tackle two questions. First, how do variational and stochastic gradient methods for experimental design (that I have previously worked) on translate into the model selection context? And second, how do these methods intersect with a recently proposed classification-driven approaches to experimental design for model selection by Hainy et al.? If you’re not familiar with these papers, never fear, we will introduce the key concepts as we go.
Announcing a New Framework for Designing Optimal Experiments with Pyro
Adam Foster, Martin Jankowiak. Uber Engineering Blog.
Experimentation is one of humanity’s principal tools for learning about our complex world. Advances in knowledge from medicine to psychology require a rigorous, iterative process in which we formulate hypotheses and test them by collecting and analyzing new evidence. At Uber, for example, experiments play an important role in the product development process, allowing us to roll out new variations that help us improve the user experience. Sometimes, we can rely on expert knowledge in designing these types of experiments, but for experiments with hundreds of design parameters, high-dimensional or noisy data, or where we need to adapt the design in real time, these insights alone won’t necessarily be up to the task.
To this end, AI researchers at Uber are looking into new methodologies for improving experimental design. One area of research we’ve recently explored makes use of optimal experimental design (OED), an established principle based on information theory that lets us automatically select designs for complex experiments.
Predicting the outcome of a US presidential election using Bayesian Experimental Design
In this tutorial, we explore the use of optimal experimental design techniques to create an optimal polling strategy to predict the outcome of a US presidential election. In the previous tutorial, we explored the use of Bayesian optimal experimental design to learn the working memory capacity of a single person. Here, we apply the same concepts to study a whole country.
We set up a Bayesian model of the winner of the election w, as well as the outcome y of any poll we may plan to conduct. The experimental design is the number of people n to poll in each state. To set up our exploratory model, we use historical election data 1976-2012 to construct a plausible prior and the 2016 election as our test set: we imagine that we are conducting polling just before the 2016 election.
Designing Adaptive Experiments to Study Working Memory
This tutorial serves as an introduction to designing optimal experiments using Pyro. The tutorial works through a specific example of this entire optimal experimental design (OED) procedure with multiple rounds of experiments. The tutorial focuses on how to design adaptive psychology experiments to learn a participant’s working memory capacity. The design that is adapted is the length of a sequence of digits that we ask a participant to remember.